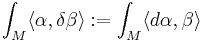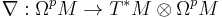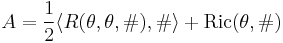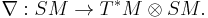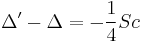Weitzenböck identity

In mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity (named after Roland Weitzenböck) expresses a relationship between two second-order elliptic operators on a manifold with the same leading symbol. Usually Weitzenböck formulae are implemented for G-invariant self-adjoint operators between vector bundles associated to some principal G-bundle, although the precise conditions under which such a formula exists are difficult to formulate. Instead of attempting to be completely general, then, this article presents three examples of Weitzenböck identities: from Riemannian geometry, spin geometry, and complex analysis.

1 Riemannian geometry
2 Spin geometry
3 Complex differential geometry
4 Other Weitzenböck identities
5 See also
6 References

Riemannian geometry

In Riemannian geometry there are two notions of the Laplacian on differential forms over an oriented compact Riemannian manifold M. The first definition uses the divergence operator δ defined as the formal adjoint of the de Rham operator d:

$\int_M \langle \alpha,\delta\beta\rangle�:= \int_M\langle d\alpha,\beta\rangle$

where α is any p-form and β is any (p+1)-form, and 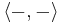$\langle -,-\rangle$ is the metric induced on the bundle of (p+1)-forms. The usual form Laplacian is then given by

Δ = dδ + δd.

On the other hand, the Levi-Civita connection supplies a differential operator

$\nabla:\Omega^pM\rightarrow T^*M\otimes\Omega^pM$

where Ω^pM is the bundle of p-forms and T^*M is the cotangent bundle of M. The Bochner Laplacian is given by

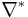$\Delta'=\nabla^*\nabla$

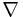where $\nabla^*$ is the adjoint of $\nabla$ .

The Weitzenböck formula then asserts that

$\Delta' - \Delta = A$

where A is a linear operator of order zero involving only the curvature.

The precise form of A is given, up to an overall sign depending on curvature conventions, by

$A=\frac{1}{2}\langle R(\theta,\theta,\#),\#\rangle %2B \text{Ric}(\theta,\#)$

where

R is the Riemann curvature tensor,
Ric is the Ricci tensor,
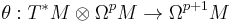$\theta:T^*M\otimes\Omega^pM\rightarrow\Omega^{p%2B1}M$ is the alternation map,
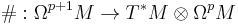$\#:\Omega^{p%2B1}M\rightarrow T^*M\otimes\Omega^pM$ is the universal derivation inverse to θ on 1-forms.

Spin geometry

If M is an oriented spin manifold with Dirac operator ð, then one may form the spin Laplacian Δ = ð² on the spin bundle. On the other hand, the Levi-Civita connection extends to the spin bundle to yield a differential operator

$\nabla:SM\rightarrow T^*M\otimes SM.$

As in the case of Riemannian manifolds, let 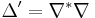$\Delta'=\nabla^*\nabla$ . This is another self-adjoint operator and, moreover, has the same leading symbol as the spin Laplacian. The Weitzenböck formula yields:

$\Delta'-\Delta=-\frac{1}{4}Sc$

where Sc is the scalar curvature. This result is also known as the Lichnerowicz formula.

Complex differential geometry

If M is a compact Kähler manifold, there is a Weitzenböck formula relating the 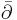$\bar{\partial}$ -Laplacian (see Dolbeault complex) and the Euclidean Laplacian on (p,q)-forms. Specifically, let

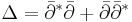$\Delta=\bar{\partial}^*\bar{\partial}%2B\bar{\partial}\bar{\partial}^*$ , and

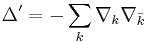$\Delta'=-\sum_k\nabla_k\nabla_{\bar{k}}$ in a unitary frame at each point.

According to the Weitzenböck formula, if α ε Ω^(p,q)M, then

Δ'α − Δα = A(α)

where A is an operator of order zero involving the curvature. Specifically, if

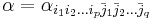$\alpha=\alpha_{i_1i_2\dots i_p\bar{j}_1\bar{j}_2\dots\bar{j}_q}$ in a unitary frame, then

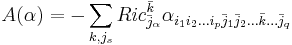$A(\alpha)=-\sum_{k,j_s} Ric_{\bar{j}_\alpha}^{\bar{k}}\alpha_{i_1i_2\dots i_p\bar{j}_1\bar{j}_2\dots\bar{k}\dots\bar{j}_q}$ with k in the s-th place.

Other Weitzenböck identities

In conformal geometry there is a Weitzenböck formula relating a particular pair of differential operators defined on the tractor bundle. See Branson, T. and Gover, A.R., "Conformist Invariant Operators, Differential Forms, Cohomology and a Generalisation of Q-Curvature", Communications in Partial Differential Equations, 30 (2005) 1611-1669.

References

Griffiths, Philip; Harris, Joe (1978), Principles of algebraic geometry, Wiley-Interscience (published 1994), ISBN 978-0471050599